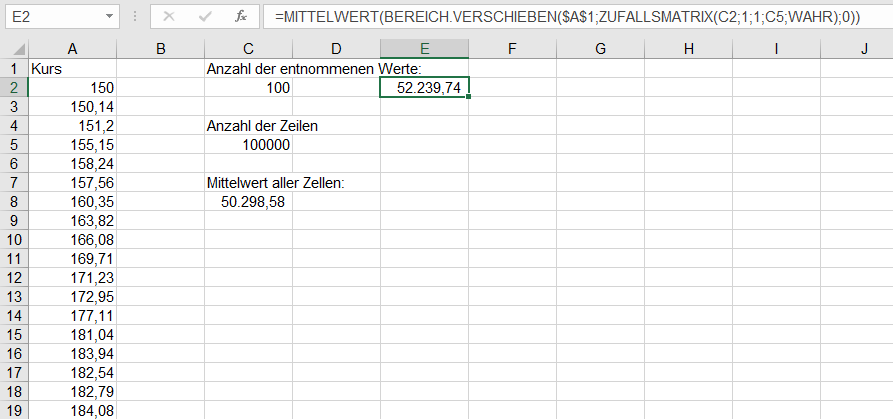
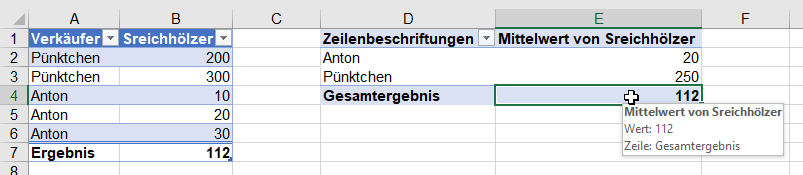
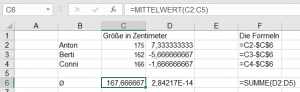
Kunden, die die Schreibtischlampe gekauft haben, haben auch Verlängerungskabel gekauft.
Vor vier Wochen war ich in einer Rechtsanwaltskanzlei und habe gefühlte 15.000 Diagramme bearbeitet. Dabei sind mir eine Reihe an Dingen aufgefallen. Beispielsweise:
Wir erstellen ein Diagramm, das die durchschnittlichen Prozesskosten berechnet. Und zwar der Jahre 2013 – 2018 und 2019 – 2020. Und daneben der Gesamtdurchschnitt. Das Diagramm sah wie folgt aus:
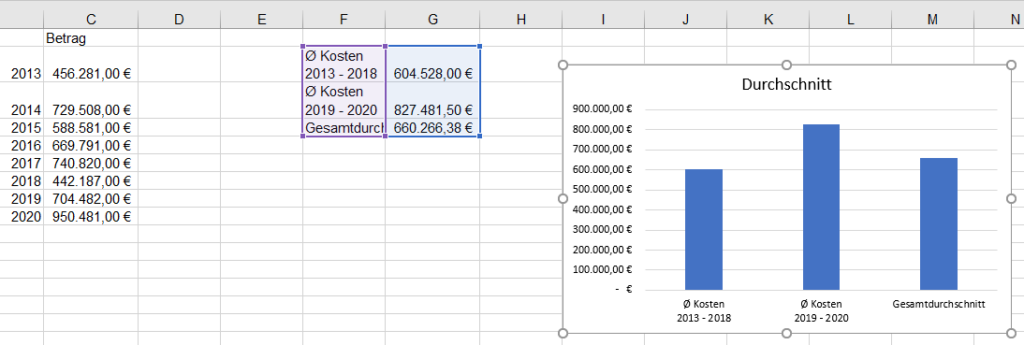
Einer der Rechtsanwälte warf einen Blick darauf und sagte, dass die Berechnung (und die Darstellung) nicht stimmen könne: der Durchschnitt der beiden Durchschnitte sei doch der Mittelwert. Im Diagramm sei er viel zu gering.
Mein Bauchgefühl sagte, dass dies nicht stimmen könne. Ich nahm ein Blatt Papier und rechnete:
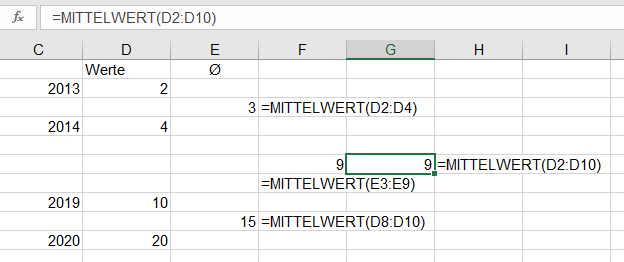
Der Durchschnitt von 2 und 4 ist 3. Der Durchschnitt von 10 und 20 ist 15. Der Durchschnitt von 3 und 15 ist 9; ebenso wie der Durchschnitt von 2, 4, 10 und 20. Sollte der Rechtsanwalt doch recht haben? Zweiter Versuch:
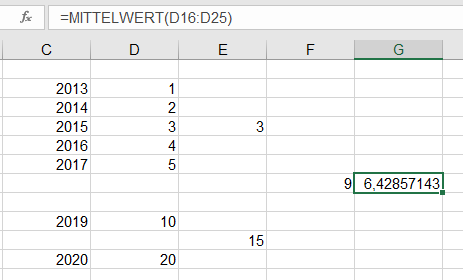
Ich berechne den Durchschnitt von 1, 2, 3, 4 und 5. Er lautet 3. Der Durchschnitt von 10 und 20 beträgt 15. Mittelwert von 3 und 15 ist 9; jedoch: Durchschnitt von 1, 2, 3, 4, 5, 10 und 20 lautet 6,42857
Stimmt: wenn die Anzahl unterschiedlich ist, ist der Durchschnitt zweier Duchschnitte eben nicht der Mittelwert aller Zahlen. Der Rechtsanwalt hat sich geschlagen gegeben. Wäre doch gelacht!