Lösungen der Knobelaufgaben
Die Schnecke
Da die Strecke, welche die Schnecke nachts herunterrutscht, in jeder Nacht größer ist als in der vorhergehenden, kann diese Aufgabe nicht im Kopf gelöst werden. In der ersten Nacht hat die Schnecke eine Höhe von 0,5 Meter erreicht. In der zweiten Nacht befindet sie sich auf 0,5 x 0,9+0,5 = 0,95. In der dritten Nacht beträgt ihre Höhe (0,5 x 0,9 + 0,5) x 0,9 + 0,5 oder 0,5 x (1 + 0,9 + 0,9²). Allgemein ist sie in der Nacht Nummer n auf 0,5 x (1 + 0,9 + 0,9² +…+ 0,9n-1).
Für die Summe
gilt:
Da q = 0,9 und a = 0,5 sind, lautet die Formel:
oder:
Daraus folgt für n:
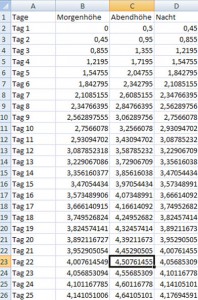
Also wird die Schnecke am 22. Tag die Mauer „bezwungen“ haben.
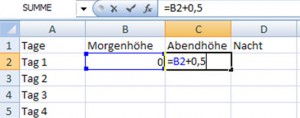
Diese Aufgabe kann dagegen leicht in Excel gelöst werden. Eine Spalte dient zur Beschrif-tung der Tage, eine Zeile zur Beschriftung der Tageszeiten. In der ersten Spalte läuft ein Zähler.
Da die Schnecke bei 0 startet, wird dies in die erste Zelle eingetragen. In der Abendhöhe steht nun die Formel Morgenhöhe + 0,5 oder: B2 + 0,5.
Werden nun von dieser Zahl 10 % abgezogen, so darf nicht C2-10 % geschrieben werden! Dies führt unweigerlich zu einem Fehler, da 10 % gleichbedeutend ist mit 0,1. Vielmehr muss 10 % von C2 abgezogen werden, also:
=C2-C2*10%
Oder einfacher: Da uns nicht die Strecke interessiert, die unsere Schnecke herunterrutscht (die 10 %), sondern die Endhöhe (die 90 %), so kann diese auch ermittelt werden über:
=C2*90%
Man könnte die beiden Werte (10 % beziehungsweise 90 % und 0,5) auch auslagern, das heißt, in andere Zellen schreiben. Dann könnte man mit einem absoluten Bezug darauf zugreifen. Dies macht Sinn, wenn man alle möglichen Schnecken berechnen wollte. Diese Morgenhöhe wird mit einem Bezug in die nächste Zeile übernommen.
Schließlich können alle drei Spalten heruntergezogen werden.
Nun braucht man nur noch nachzusehen, wann die 4,5 Meter überschritten sind. Aber in der Abendspalte, nicht in einer der Morgenspalten! Denn die Schnecke klettert von 4 auf 4,5 Meter hinauf und rutscht nicht von 5 auf 4,5 Meter herunter. Übrigens: Wäre die Mauer 5,0 Meter hoch, so würde unsere arme Schnecke nie oben ankommen!
Man könnte natürlich die beiden (oder die drei) Werte (10 %, 4,5 Meter Ziel und 0,5 Meter Kletterhöhe) in Zellen über oder neben der Tabelle auslagern und dann mit einem festen Bezug darauf zugreifen. Dann könnte man diese Werte ändern, um unterschiedliches Schneckenverhalten zu testen. Oder mit dem Szenario-Manager unterschiedliche Startwerte eingeben und in einer Tabelle nachsehen, wie hoch die Schnecke am 5., am 10., am 20. und 30. Tag ist. Das war hier aber nicht verlangt.
Ebenso war nicht verlangt, dass ab dem Tag, an dem die Schnecke ihren „Zenit“ erreicht hat, die Werte automatisch ausgeblendet werden. Es funktioniert mit einer Wenn-Funktion, die in Kapitel 8.1 erläutert wird. Damit könnte der Benutzer unterschiedliche Werte eingeben, und die Reihe wird so lange angezeigt, bis der Zielwert erreicht ist. Ein vernünftiges und praktisches Beispiel hierfür finden Sie in Kapitel 11. Dort werden in einer Tabelle alle Werte ausgeblendet, die nicht mehr interessant sind (beispielsweise wenn eine Schuld zurückbezahlt ist).
Auf dem Markt
Eine hübsche Aufgabe, die man „von hinten“ im Kopf berechnen kann. Oder mit Hilfe einer Gleichung:
Oder auch mit der Zielwertsuche. Oder einfacher, indem man in eine Zelle A2 den Wert 1 eingibt und daneben berechnet:
=((((((A2/2-1)/2-1)/2-1)/2-1)/2-1)/2-1)
Lässt man die 1 durch Ziehen „hochzählen“, dann kann das Ergebnis 126 schnell gefunden werden.
Fronleichnam
Diese Aufgabe könnte man in Excel sicherlich durch Ziehen einer Zahlenreihe lösen. Leichter ist es, wenn man auf einem Blatt Papier oder mit der Excel-Funktion das kleinste gemeinsame Vielfache von 10, 9, 8, 7, 6, 5, 4, 3 und 2 ermittelt. Es lautet 2.520. Bei 2.519 Teilnehmern des Festzugs wäre es also zu oben beschriebenem Problem gekommen. Allerdings auch beim Doppelten: Auch 5.039 wäre eine Lösung. Die nächstgrößere Zahl 7.559 überschreitet die Bedingung, dass die Zahl kleiner als 7.000 sein muss.
Schließlich wird noch erwähnt, dass „es mit 11 nicht aufgehen würde“. Da aber 2.519 durch 11 ohne Rest teilbar ist, muss die Lösung 5.039 sein.
Pleite statt Glückssträhne
Diese Aufgabe kann im Kopf gelöst werden. Hat der Spieler nach vier Runden kein Geld mehr, dann hatte er zuvor dem Croupier 100 Euro geschenkt. Davon hat er die Hälfte gewonnen, das heißt zu Beginn der vierten Runde hatte er 50 Euro. Zuvor hat er 100 Euro verschenkt (ergibt 150) und davon die Hälfte gewonnen (75). Und so weiter. Oder Sie lösen die Gleichung
(((x × 2 – 100) × 2 – 100) × 2 – 100) × 2 – 100 = 0
nach x auf.
In Excel wird die Aufgabe wie folgt gelöst: Wir wissen den Einsatz nicht, also können wir mit einem beliebigen Einsatz durchkalkulieren. Beispielsweise mit 200 Euro. Hätte unser Spieler 200 Euro gehabt, so hätte er nach vier Runden 1.700 Euro. In der ersten Zelle wird ein Wert eingetragen (200), in der Zelle daneben verdoppelt (=B2*2). Von diesem Ergebnis wird 100 abgezogen (=C2-100). Dieses Ergebnis wird in die nächste Zeile übernommen: =D2. Nun können die drei Rechnungen heruntergezogen werden.
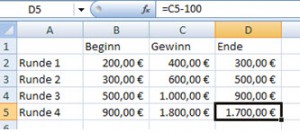
Anschließend wird zurückgerechnet. Dafür ist die Zielwertsuche hilfreich. Das Endkapital soll 0 sein, gesucht ist der Anfangswert. In der Zielwertsuche ist bei „Zielzelle“ die Zelle anzugeben, in der das Ergebnis steht. Dort soll der „Zielwert“ 0 betragen. Gesucht ist dagegen die „Veränderbare Zelle“ des Anfangswerts.
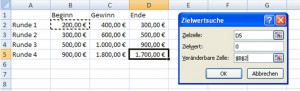
Das „Zurückrechnen“ liefert das Ergebnis 93,75. Damit hat der Spieler nach vier Runden kein Geld mehr.
Melonen
Diese Aufgabe kann man mit vier Gleichungen mit vier Unbekannten lösen. Angenommen G1 sei das Gewicht der kleineren Melone, E1 ihr Preis. Dann ist G2 das Gewicht der größeren Melone und E2 ihr Preis. Daraus ergibt sich:
(I) G1 + G2 = 20
(II) E1 + 0,2 = E2
(III) G1 E1 = 2
(IV) G2 E2 = 11,20
Löst man die Gleichungen nach G2 (oder G1) auf, so erhält man eine quadratische Gleichung, deren eine Lösung 70 (oder -50) beträgt und damit über dem Gesamtgewicht liegt (oder nicht realistisch ist).
Löst man die Aufgabe in Excel, so könnte man die Zellen E1, E2, G1 und G2 verwenden. Angenommen in G1 steht das Gewicht 5. Dann berechnet sich G2 durch =20-G1. Daraus folgt der Preis in E1: =2/G1, und der Preis in E2: =11,2/G2. Die Differenz der Preise wird in eine fünfte Zelle geschrieben. Sie berechnet sich als =E2-E1 und ergibt für das angenommene Gewicht G1 die Zahl 0,34666. Die Differenz soll allerdings 0,2 betragen.
Dafür wird die Zielwertsuche verwendet, die in dieser Zielzelle den Zielwert 0,2 haben soll. Die veränderbare Zelle ist G1. Die Werte werden berechnet und liefern 4,00442490618633 und 15,9955750938137. Verwendet man den Solver, dann erhält man die korrekten Zahlen 4 und 16.
Die Wahl
Diese Aufgabe kann man im Kopf lösen. Addiert man die drei Differenzen, so erhält man 125 Stimmen, die der Sieger mehr als seine Gegner erhalten hat. Addiert man nun diese Summe zur Gesamtzahl 6.095, so ergibt sich 6.220. Diese Zahl geteilt durch die Anzahl der Kandidaten ergibt die Stimmenzahl des Siegers, nämlich 1.555.
Oder als Gleichung:
G+(G–22)+(G–30)+(G–73) = 6.095
In Excel wird in die Zelle G1 eine fiktive Zahl eingegeben. In den Zellen G2, G3 und G4 werden die Differenzen berechnet: =G1-22, =G1-30 und =G1-73. Darunter wird die Summe gezogen. Nun kann mit Hilfe der Zielwertsuche in der Summenzelle der korrekte Zielwert 6.095 berechnet werden, wenn die veränderbare Zelle G1 ist.
Mit gesundem Menschenverstand
Der Vater überlegte folgendermaßen: Das Alter des Kindes darf nicht geringer als drei Jahre sein, und es darf, nach der Bedeutung des Wortes „Kind“, nicht höher als 15 Jahre sein. Folglich wird das Kind nach drei Jahren nicht weniger als sechs und nicht mehr als 18 Jahre alt sein. Zwischen den Zahlen sechs und 18 gibt es nur zwei Zahlen, aus denen sich die Quadratwurzel ziehen lässt: neun und 16. Und bei 16 stimmt die Probe nicht. Folglich beträgt das Alter des Kindes sechs Jahre.
Die Studentin hatte folgende Lösung im Auge: Es sei a das Alter des Kindes. Dann gilt:
Dies ergibt die beiden Lösungen 1 und 6. Allerdings erfüllt nur die Zahl 6 die Gleichung.
Steht in Excel in einer Zelle, beispielsweise C1, eine Alterszahl, beispielsweise 7, dann ergibt die Rechnung
=(C1+3)^0,5+3-C1
den Wert –0,83772233983162. Er wird nun mit Hilfe der Zielwertsuche auf 0 zurückgerechnet.
Wie alt ist die Mutter?
Der Vater wird doppelt so alt sein wie der Sohn, wenn man weiß, wie alt der Vater bei seiner Geburt war. Diese Zahl ergibt sich aus der Differenz der Lebensalter. Wird sie verdoppelt, dann liegt diese Zahl vor. Wird von dieser Zahl das jetzige Vater-Alter abgezogen, dann weiß man, wann das Ereignis eintreten wird. Diese Differenz kann mit drei multipliziert werden und zu den jetzigen Altern des Vaters, der Mutter und des Sohns addiert werden. Daraus ergeben sich:
(I) AlterV = AlterS × 6
(II) AlterM = 96 – AlterV – AlterS
(III) ((AlterV – AlterS) × 2 – AlterC) × 3 + AlterV + AlterM + AlterS = 192
Dies kann nach AlterM aufgelöst werden, oder man trägt in Excel die Werte ein. In M1 steht das Alter des Vaters, beispielsweise 60. In M2 steht das Alter der Mutter, nämlich
=96-M1-M3
und in M3 das Alter von Andreas, dem Sohn:
=M1/6
Daneben wird berechnet:
=((M1–M3)*2–M1)*3+M1+M2+M3
Nun kann mit der Zielwertsuche ausgerechnet werden: der Zielwert der Formel lautet 192, veränderbar ist die Zelle M1. Und so ergibt sich das Alter der Mutter: 40 Jahre.
Die Waage
Die Aufgabe kann leicht im Kopf oder durch Aufstellen von drei Gleichungen gelöst wer-den:
(I) GHäberle = GHund + GBaby + 100
(II) GHund = GBaby / 2
(III) GHäberle + GHund + GBaby = 148
Oder über eine Zielwertsuche. Wird ein fiktives Hundegewicht in H1 eingetragen, so berechnet sich das Gewicht des Babys über
=H1*2
Das Gewicht von Frau Häberle beträgt
=H1+H2+100
Und die Summe lautet:
=SUMME(H1:H3)
Sie soll allerdings den Zielwert 148 haben, veränderbar ist natürlich das Gewicht des Hundes.
Die Jedi-Ritter
Es wird eine Zahl gesucht, deren Quadrat multipliziert mit 13 und um 1 vergrößert wieder eine Quadratzahl ergibt. Das allgemeine Problem wurde zuerst von Fermat vorgestellt, obwohl es auch als Pell’sche Gleichung bekannt wurde. Es handelt sich um eine Diophantische Gleichung 2. Grades (benannt nach dem griechischen Mathematiker Diophantos von Alexandria aus dem 3. Jahrhundert vor Chr.):
x²–Dy² = 1
Sie ist nicht mit einfachen Mitteln der Algebra zu lösen. Entweder man „probiert“, oder man greift gleich zu Excel:
In der Zelle B2 steht die Anzahl der Ritter pro Quadrat, beispielsweise 10. In der Zelle da-neben wird die Gesamtstärke des Heeres berechnet über:
=B2^2*13+1
In der Zelle B3 steht die Stärke des gesamten Heeres, beispielsweise 100, daneben das Ergebnis des Quadrats: =B3^2
Die Differenz
=C3-C2
wird darunter gebildet. Sie muss 0 sein.
Die Zielzelle soll den Zielwert 0 haben, veränderbare Zellen sind B2 und B3. Die Nebenbedingungen lauten, dass B2 und B3 >=1 und dass B2 und B3 ganzzahlige Ergebnisse sein müssen. Der Solver findet nach circa 700 Rechenoperationen die Lösung: Die Quadrate bestehen aus 180 Rittern pro Seite, das ergibt 421.200 Ritter. Die Wurzel aus 421.201 beträgt 649, wie leicht abgelesen werden kann.
In einem anderen Rätselbuch fand sich die gleiche Aufgabe mit 61 Quadraten. Hier ermittelt der Solver nach mehreren tausend Rechnungen 60.158 Ritter pro Seitenlänge. Kommt der Boss hinzu, so hat das Quadrat 469.849 Ritter pro Seitenlänge. Das Quadrat ergibt 220.758.082.801. Erstaunlicherweise findet sich in diesem Rätselbuch die nächstgrößere Lösung als die kleinste:
226.153.980^2 + 1 = 1.766.319.049^2 = 3.119.882.982.860.260.000
Der Ausflug
Die Aufgabe kann schnell mit zwei algebraischen Gleichungen gelöst werden. Es sei w die Anzahl der Wagen und p die Anzahl der Personen bei der Ausfahrt. Dann gilt:
(I) w × p = (w–10) × (p+1)
(II) w × p = (w–25) × (p+3)
Ebenso können diese Werte und Formeln in Excel eingegeben werden. In B2 steht eine fiktive Personenzahl 10, und in B3 steht die angenommene Wagenzahl 50. Der Beginn berechnet sich als
=B1*B2
Nach dem ersten Unglück lautet die Formel
=(B2-10)*(B1+1)
Und nach dem zweiten Zusammenbruch
=(B2-25)*(B1+3)
Die Differenz aus dem ersten Wert lautet beispielsweise
=B4-B5
die andere Differenz
=B5-B6
Damit die erste und die zweite Differenz den Wert 0 haben kann, muss im Solver für die erste Zielzelle der Zielwert auf 0 gesetzt, und als Nebenbedingung die zweite Zelle auf 0 gelegt werden. Die veränderbaren Zellen sind B1 und B2.
Der korrekte Wert – 100 Wagen und insgesamt 9 Personen – ist schnell ermittelt.
Pilze
Auch diese Aufgabe kann man (fast) im Kopf lösen. Oder mit Hilfe eines Gleichungssystems.
In Excel könnte man die Aufgabe wie folgt lösen:
In vier Zellen werden vier beliebige Werte eingegeben, beispielsweise 10, 10, 10 und 15. Darunter wird die Summe gezogen. Daneben wird gerechnet: +2, -2, /2 und *2. Im Solver kann man nun einstellen, dass die Zielzelle (Summe) 45 betragen muss, veränderbar sind die vier einzelnen Zellen und mit drei Nebenbedingungen erste berechnete Zahl = zweite berechnete Zahl, zweite berechnete Zahl = dritte und dritte = vierte löst der Solver die Aufgabe und liefert die vier Zahlen 12, 8, 20 und 5.
Briefmarken
Auch diese Aufgabe könnte man im Kopf lösen. Da die Dame zehnmal so viele Marken zu einem Euro wie zu zwei Euro haben möchte, wird sie insgesamt ein Vielfaches von 12 Euro ausgeben. Die Differenz zwischen 100 und dieser Zahl muss durch 5 teilbar sein. Also bleibt nur 5 × 12. Oder anders ausgedrückt:
x × 2 Euro + x × 10 × 1 Euro + y × m = 100
liefert eindeutige ganzzahlige Werte.
In Excel stehen wieder die beiden Werte für x und y in zwei Zellen (I1 und I2). Dann wird berechnet:
=I1*2+I1*10*1+I2*5
Der Zielwert dieser Zelle beträgt 100, die Randbedingungen für die beiden anderen Zellen lauten:
>=0, <=100 und ganzzahlig.
Mehr Aufgaben
Die oben gestellten Aufgaben sind sicherlich nicht alle Knobelaufgaben, die man mit (und ohne) Excel lösen kann. Schlagen Sie ein beliebiges Rätselbuch auf – dort werden Sie sicherlich Aufgaben des folgenden Typs finden:
* Bei meinem letzten Besuch in Costa Rica erzählte mir Juan, dass 20 Regimente kontinuierlich aufgestellt wurden, und zwar in fortlaufendem Prozess, bei dem jede Woche jedem Regiment 100 Mann hinzubeordert wurden. Am Ende jeder Woche wurde dasjenige Regiment, das am meisten Männer zählte, an die Front geschickt.
Nun trug es sich zu, dass zu der Zeit, zu der das 1. Regiment 1000, das 2. 950, das 3. 900 zählte – und so fort, mit einer jeweiligen Verminderung von 50 bis hin zum 20. mit nur 50 Mann, Offizier Juan herausfand, dass der Oberst des 5. Regiments (das 800 Mann stark war) ausgezeichnet Schach spielte. Daher gab er dessen Regiment, um es nicht an die Front schicken zu müssen, was in fünf Wochen der Fall gewesen wäre, statt 100, wie den anderen, jede Woche nur 30 Mann.
Angenommen es werden fortwährend 20 Regimente aufgestockt, nach wie vielen Wochen muss sich der Schach spielende Oberst an den Kriegsschauplatz begeben?
* Eine einzelne Wildgans begegnet einem Schwarm Wildgänse. Sie rief: „Guten Tag, ihr hundert Gänse!“ Die alte Leitgans antwortete ihr: „Nein, wir sind nicht hundert Gänse! Schau an, wenn wir so viele wären, wie wir sind, und dann noch einmal so viel und dann noch einhalbmal so viel und noch ein viertelmal so viel und dann du dazu, dann wären wir hundert Gänse, aber so sind wir … na, rechne selbst, wie viele wir sind.“
* Drei Brüder hatten 72 Äpfel bekommen, wobei jedem unterschiedlich viele Äpfel zugeteilt wurden. Der Jüngste, ein kluges Kerlchen, schlug den Brüdern folgenden Tausch vor:
„Unser ältester Bruder gibt jedem von uns so viele Äpfel, wie wir bereits haben. Dann gibt der mittlere Bruder uns so viele Äpfel, wie jeder hat, und zum Schluss werde ich je-dem so viele Äpfel geben, wie jeder hat.“ Ohne dass die Brüder eine Hinterlist vermuteten, willigten sie ein. Am Ende hatte jeder die gleiche Menge. Wie viele Äpfel hatten sie zu Beginn der Tauschaktion?
* Drei Jäger verteilen ihre Patronen zu gleichen Teilen unter sich. Nachdem jeder Jäger vier Schuss abgegeben hatte, besaßen sie zusammen noch so viele Patronen, wie nach der Verteilung jeder einzelne gehabt hatte. Wie viele waren das?
* Ein Hausierer läutet in einem Wohnhaus im obersten Stock an einer Türe. Eine Dame öffnet und teilt ihm mit, dass sie nichts kaufen möchte. Doch er bittet sie inständig darum, worauf sie weich wird. „Gut“, sagt sie, „ich kaufe Ihnen etwas ab, wenn Sie mir sagen können, wie alt meine drei Töchter sind. Das Produkt ihrer Alter ist 36 und die Summe gleich meiner Hausnummer.“
Der Hausierer überlegt und antwortet: „Sie haben mir eine Information unterschlagen!“ „Stimmt“, meint sie, „meine älteste Tochter spielt Klavier.“ Nun weiß der Hausierer die Lösung. Wie alt sind die Töchter?
* Horst wird gefragt, wie alt seine vier Kinder sind. Er gibt als Antwort: „Das Produkt ihrer Alter beträgt 1.536, die Summe 30“. Er überlegt und fügt hinzu: „Die Jüngste heißt Claudia.“ Wie alt sind seine Kinder?
Oder noch schwieriger:
* „Ich habe gestern meinen Geburtstag mit meiner Frau und meinen beiden Nichten gefeiert“, erzählt der Professor. „Es fiel mir auf, dass die drei Damen zusammen genau zweimal so alt sind wie ich. Wenn man die Alter der drei Damen miteinander multipliziert, ergibt sich 2.450. Können Sie mir sagen, wie alt meine beiden Nichten sind?“
Der Assistent überlegte und antwortete: „Sie haben mir nicht genügend erzählt.!“
„Da haben Sie recht“, sagte der Professor, „aber wenn ich Ihnen nun sage, dass ich der Älteste von uns vieren war, so wissen Sie alles Nötige.“ Wie alt ist der Professor?
* Für welche Werte von n ist N(n) eine Quadratzahl?
* Ich wollte die Entfernung von meinem Haus bis zu dem meines Freundes feststellen. Ich ging daher mit gleichmäßigen Schritten und zählte auf der ersten Hälfte des Weges die Doppelschritte und auf der zweiten Hälfte jeden dritten Schritt. Dabei ergaben sich 250 Doppelschritte mehr als dreifache Schritte. Wie viele Schritte waren es bis zum Haus meines Freundes?
* Wie groß ist die Summe der Quersummen aller Zahlen von 1 bis 1.000.000?
* Drei Bauern kamen an einen Gasthof , wo sie sich ausruhen und zu Mittag essen wollten. Sie sagten der Wirtin, sie möge ihnen Kartoffeln kochen, selber aber schleifen sie ein. Die Wirtin tat, wie ihr geheißen, weckte ihre Gäste jedoch nicht, sondern stellte die Schüssel mit dem Essen auf den Tisch. Einer der Bauern erwachte, sah die Schüssel, und weil er seine Gefährten nicht wecken wollte, aß er seinen Anteil und legte sich wie-der schlafen. Bald darauf wachte der zweite Bauer auf, aß ein Drittel der verbleibenden Kartoffeln und schlief wieder ein. Da erwachte der dritte und aß ebenfalls den dritten Teil davon. In dem Moment wurden die anderen beiden wach und sahen, dass noch acht Kartoffeln in der Schüssel verblieben waren. Wie viele Kartoffeln hatte die Wirtin auf den Tisch gebracht?
* Es brennen zwei Kerzen von ungleicher Länge und verschiedener Stärke. Die längere brennt in 3 ½ Stunden herunter, die kürzere in 5 Stunden. Nach 2 Stunden Brenndauer haben die Kerzen die gleiche Länge. Wie viel war die eine anfangs kürzer als die andere?
* Welche Zahlen können als Summe zweier Quadratzahlen geschrieben werden? Also: 13 = 3 3 + 2 2. Mit 417 geht das nicht. Allerdings mit 317 und 617.
* In einem Dartclub hängt eine Zielscheibe mit den Punkten 1, 2, 3, 5, 10, 20, 25 und 50. Einer der Schützen kam mit sechs Wurf auf 96, davon war eine Dublette, das heißt, zwei Pfeile trafen den gleichen Ring.
Wie muss man werfen, damit man mit drei Dubletten eine Gesamtpunktzahl von 96 erzielt?
Oder schlagen Sie ein Schulbuch auf. Dort finden Sie sicherlich Aufgaben des Typs:
* Angenommen es soll eine Fahrt mit einem Auto unternommen werden, die eine Strecke von 600 km umfasst. Als Fahrer wird ein Student gewonnen, der pro Stunde 15 Euro erhält. Nun ist der Benzinverbrauch (gemessen in 1/100 km) abhängig von der Geschwindigkeit – in unserem Falle ergibt sich:
Angenommen, der Benzinpreis liegt bei 1,40 Euro, so berechnen sich die Benzinkosten über:
Das heißt: Bei einer Geschwindigkeit von 100 km/h kostet die Fahrt 108,62 €, bei 150 km/h dagegen nur noch 87,71 €. Bei welcher Geschwindigkeit wird die Fahrt am billigsten?
Zu all diesen Aufgaben liegt keine Lösung dem Buch bei – der geneigte Leser möge sich bitte die Mühe machen, diese (recht einfachen) Formeln in eine leere Excel-Tabelle einzugeben und mit Hilfe der Zielwertsuche und des Solvers zu lösen.
Die Aufgaben wurden folgenden Büchern entnommen (und zum Teil abgeändert).
Engel, Michael: Denksport-Rätsel für Geniale. Wien: öbv & hpt 2003
Hemme, Heinrich: Heureka. Unterhaltsame Mathematik in 95 Rätseln. 2. Auflage: Göttingen: Vandenhoeck und Rupprecht 2001
Herrmann, Norbert: Mathematik ist überall. Mathematik im Alltag / alltägliche Mathematik. München 2005
Ignatjew, Emel’an I: Mathematische Spielereien. 2. Auflage. Frankfurt/Main: Deutsch-Taschenbücher 1992 (Е. И. Игнатьев: В царстве смекалки. Издательство „Наука“, Москва 1979)
Loyd, Sam, Gardner, Martin: Mathematische Rätsel und Spiele. Denksportaufgaben für kluge Köpfe. 14. Auflage. Köln: DuMont 1999

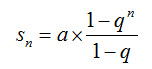
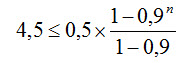
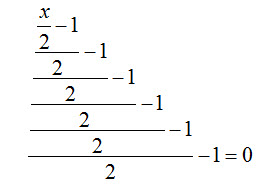
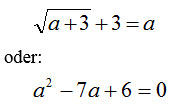
Ich bekomme für die Melonen ein anderes Ergebnis heraus: 17,6 und 2,4 Pfund. Der Fehler auf der Website ist, dass der Preis der größeren Melone hier als größer pro Pfund angenommen wurde…
Das ist korrekt, Andreas – ich muss das Beispiel korrigieren. Meine Lösung ist nur dann korrekt, wenn die größere Melone um 0,2 Euro TEURER ist als die kleinere. Nicht umgekehrt.
Danke fürs genaue Mitlesen und Mitknobeln.
Rene
Wir haben zur Dublettenbereinigung ein richtiges Unternehmen beauftragt. Es haben sich in den Jahren so viele Datensätze angesammelt, die bereinigt werden müssen. Das soll ruhig einer machen, der darauf spezialisiert ist.
Hallo,
ich bin mit der Lösung bei dem Ausflug nicht einverstanden.
Abgesehen davon, wie man 900 Personen in 10 Wagen bringen soll, bleibt das Problem, dass von 10 Wagen nicht 25 kaputt gehen können.
Ich bin auf folgendes Ergebnis gekommen:
Zu Beginn des Ausfluges sind je 3 Leute in insgesamt 50 Wagen gefahren.
Am Ende des Ausfluges saßen jeweils 6 Leute in 25 übrigen Wagen.
Auf dem Picknick waren also 150 Personen.
Liebe Grüße,
Jacob
Ja – das ist richtig – ich habe mich vertippt. Die korrekte Lösung lautet natürlich: 100 Wagen und 9 Personen. Beim ersten Unfall: 90 Wagen und 10 Personen und schließlich: 75 Wagen und 12 Personen.